Answer:
- the mass flow rate of air is 7.53 kg/s
- the exit area is 0.108 m²
Step-by-step explanation:
Given the data in the question;
lets take a look at the steady state energy equation;
m" = W"
 / [ (h₁ - h₂ ) -
/ [ (h₁ - h₂ ) -
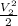 ]
]
Now at;
T₁ = 900K, h₁ = 932.93 k³/kg
T₂ = 500 K, h₂ = 503.02 k³/kg
so we substitute, in our given values
m" = [ 3200 kW ×
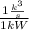 ] / [ (932.93 - 503.02 )k³/kg -
] / [ (932.93 - 503.02 )k³/kg -
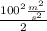 |
|
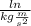 ||
||
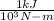 | ]
| ]
m" = 7.53 kg/s
Therefore, the mass flow rate of air is 7.53 kg/s
now, Exit area A₂ = v₂m" / V₂
we know that; pv = RT
so
A₂ = RT₂m" / P₂V₂
so we substitute
A₂ = {[
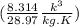 ×
×
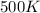 ×
×
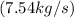 ] / [(1 bar)(100 m/s )]} |
] / [(1 bar)(100 m/s )]} |
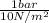 ||
||
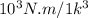
A₂ = 0.108 m²
Therefore, the exit area is 0.108 m²