Answer:
3.91 s
Step-by-step explanation:
From the question,
The height of the helicopter is given as
h = 3t²......................... Equation 1
After 5 seconds, The height of the helicopter is given as
h = 3(5²)
h = 3×25
h = 75 m.
Note: The small mailbag falls under gravity.
Hence,
h = ut + 1/2(gt²)....................... Equation 2
Where u = initial velocity of the mailbag, t = time, h = height, g = acceleration due to gravity of the mail bag.
Given: h = 75 m, u = 0 m/s ( at the maximum height).
Constant: g = 9.8 m/s²
Substitute these values into equation 2
75 = 0(t) +1/2(9.8t²)
solve for t
1/2(9.8t²) = 75
4.9t² = 75
t² = 75/4.9
t² = 15.31
t =
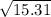
t = 3.91 s