Question

Weight gain during pregnancy. In 2004, the state of North Carolina released to the public a large data set containing information on births recorded in this state. This data set has been of interest to medical researchers who are studying the relationship between habits and practices of expectant mothers and the birth of their children. The following histograms show the distributions of weight gain during pregnancy by 837 younger moms (less than 35 years old) and 143 mature moms (35 years old and over) who have been randomly sampled from this large data set. The average weight gain of younger moms is 30.67 pounds, with a standard deviation of 14.69 pounds, and the average weight gain of mature moms is 28.52 pounds, with a standard deviation of 13 pounds. Do these data provide strong evidence that there is a significant difference between the two population means

Answer 1

To assess the significant difference in weight gain between two age groups of pregnant mothers, a statistical hypothesis test is conducted, comparing their means and standard deviations using a two-sample t-test, while accounting for factors that contribute to pregnancy weight gain.

Step-by-step explanation:

The student's question concerns whether the data on weight gain during pregnancy amongst two different age groups of mothers provides strong evidence that there is a significant difference between the two population means. To answer this, we must conduct a hypothesis test for the difference between two means. This involves calculating a test statistic, which compares the observed difference in means to the difference that might be expected by chance, and determining the p-value, which is the probability of observing a difference as extreme as, or more extreme than, the observed difference if the null hypothesis were true (i.e., there is no difference between the population means).

In the context of weight gain during pregnancy, it's known that during the second and third trimesters a pregnant person only needs to consume an additional 300 calories per day, supporting a weight gain of about 0.45 kg (1 lb) per week. Contributing factors to weight gain include not only the growing fetus, but also the enlarged uterus, amniotic fluid, and placenta, increased blood volume, and additional breast tissue.

To determine if the difference in average weight gain between the younger moms (< 35 years old) and mature moms (35 years old and over) is statistically significant, we must look at the means and standard deviations provided, and apply the appropriate statistical test, often a two-sample t-test, considering our sample sizes and variances. Given that the average weight gain of younger moms is 30.67 pounds with a standard deviation of 14.69 pounds, and the average weight gain of mature moms is 28.52 pounds with a standard deviation of 13 pounds, we must first verify assumptions such as normality and equal variances before proceeding with the t-test.

Answer 2

From the given data, there is not enough evidence to prove that there is a statistically significant difference between the two population means

Step-by-step explanation:

The number of younger moms, in the study = 837

The average weight gain of younger moms,
`\overline x`₁ = 30.67 pounds

The standard deviation of the weight gain of younger moms, s₁ = 14.69 pounds

(30.67 - 28.52)/√((14.69^2)/837 + 13²/143))

The number of younger moms, in the study = 143

The average weight gain of mature moms,
`\overline x`₂ = 28.52 pounds

The standard deviation of the weight gain of mature moms, s₂ = 13 pounds

The test statistic for the difference in two populations is given as follows;

`t=\frac{(\bar{x}_(1)-\bar{x}_(2))}{\sqrt{(s_1^(2) )/(n_(1))-(s _(2)^(2))/(n_(2))}}`

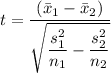
Therefore, we get;

`t=\frac{(30.67-28.52)}{\sqrt{(14.69^(2) )/(837)-(13^(2))/(143)}} \approx 1.7919`

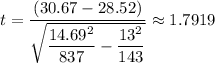
The test statistic ≈ (1.7919)

Using a graphing calculator, we get;

The critical-t = ±1.971379, p = 0.07459697

Therefore, given that the test statistic, (1.7919), < critical-t (0.07459697), we fail to reject the null hypothesis, therefor, the given data does not provide convincing evidence that there is a significant difference between the two population means