Given:
The sequence is 8, 10, 12.5, 15.625,...
To find:
The explicit formula for the given sequence.
Solution:
We have,
8, 10, 12.5, 15.625,...
Here, the first terms is 8.

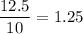

The common ratio is 1.25. So, the given sequence is a geometric sequence.
The explicit formula for a geometric sequence is:
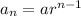
Where, a is the first term and r is the common ratio.
The explicit formula for the given geometric sequence is:
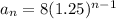
Therefore, the correct option is A.