Question

Part A

What is the explicit formula the sequence 8,10,12.5,15.625...?

Answer 1

The explicit formula for the sequence is:

`\[ a_n = 8 \cdot (1.25)^((n-1)) \]` which will generate the terms of the sequence for any positive integer value of
`\(n\)`.

To find the explicit formula for the given sequence, let's first analyze the pattern. It looks like the sequence is generated by multiplying each term by a common ratio. In this case, the common ratio appears to be
`\(1.25\)`, as each term is
`\(1.25\)` times the previous term.

The general form of a geometric sequence is given by:

`\[ a_n = a_1 \cdot r^((n-1)) \]`

where:

-
`\(a_n\)` is the
`\(n\)`-th term,

-
`\(a_1\)` is the first term,

-
`\(r\)` is the common ratio,

-
`\(n\)` is the term number.

For the given sequence
`\(8, 10, 12.5, 15.625, \ldots\)`, we can see that:

-
`\(a_1 = 8\)`,

-
`\(r = 1.25\)` (since each term is
`\(1.25\)` times the previous term).

Answer 2

Given:

The sequence is 8, 10, 12.5, 15.625,...

To find:

The explicit formula for the given sequence.

Solution:

We have,

8, 10, 12.5, 15.625,...

Here, the first terms is 8.

`(10)/(8)=1.25`

`(12.5)/(10)=1.25`

`(15.625)/(12.5)=1.25`

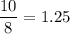
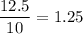
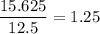
The common ratio is 1.25. So, the given sequence is a geometric sequence.

The explicit formula for a geometric sequence is:

`a_n=ar^(n-1)`

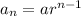
Where, a is the first term and r is the common ratio.

The explicit formula for the given geometric sequence is:

`a_n=8(1.25)^(n-1)`

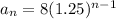
Therefore, the correct option is A.