Answer:
(a) The distance up the slope the wagon moves before coming to rest is approximately 21.74 m
(b) The distance the wagon comes to rest from the starting point is approximately 12.06 m
(c) The value of 'U' at which the wagon should be propelled if it is to come finally to rest at its starting point is approximately 3.214 m/s (the difference in value can come from calculating processes)
Step-by-step explanation:
The wagon motion parameters are;
The mass of the wagon, m = 7,200 kg
The initial velocity with which the wagon is projected along the horizontal rail, v = U
The length of the horizontal portion of the rail = 100 m
The angle of inclination of the inclined portion of the rail, θ = sin⁻¹(0.01)
The exerted frictional resistance to motion of the rail,
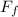 = 140 N
= 140 N
∴ θ = sin⁻¹(0.01)
The work done by the frictional force on the horizontal portion of the rail = 140 N × 100 m = 14,000 J
(a) If U = 3 m/s, we have;
Kinetic energy = 1/2·m·v²
The initial kinetic energy of the wagon, K.E. is given with the known parameters as follows;
K.E. = 1/2 × 7,200 kg × (3 m/s)² = 32,400 J
The energy, E, required to move a distance, 'd', up the slope is given as follows;
E =
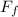 × d + m·g·h
× d + m·g·h
Where;
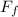 = The friction force = 140 N
= The friction force = 140 N
m = The mass of the wagon = 7,200 kg
g = The acceleration due to gravity ≈ 9.81 m/s²
h = The height reached = d × sin(θ) = d × 0.01
Therefore;
E = 140 N × d₁ + 7,200 kg × 9.81 m/s² × d₁ × 0.01 = 846.32 N × d
The energy,
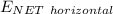 , remaining from the horizontal portion of the rail is given as follows;
, remaining from the horizontal portion of the rail is given as follows;
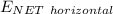 = Initial kinetic energy of the wagon - Work done on frictional resistance on the horizontal portion of the rail
= Initial kinetic energy of the wagon - Work done on frictional resistance on the horizontal portion of the rail
∴
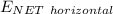 = 32,400 J - 14,000 J = 18,400 J
= 32,400 J - 14,000 J = 18,400 J
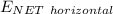 = 18,400 J
= 18,400 J
Therefore, for the wagon with energy,
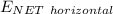 to move up the train, we get;
to move up the train, we get;
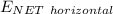 = E
= E
∴ 18,400 J = 846.32N × d
d₁ = 18,400 J/(846.36 N) ≈ 21.7401579 m
d₁ ≈ 21.74 m
The distance up the slope the wagon moves before coming to rest, d₁ ≈ 21.74 m
(b) Given that the initial velocity of the wagon, U = 3 m/s, the distance up the slope the wagon moves before coming to rest is given above as d₁ ≈ 21.74 m
The initial potential energy, PE, of the wagon while at the maximum height up the slope is given as follows;
P.E. = m·g·h = 7,200 kg × 9.81 m/s² × 21.74 × 0.01 m = 15,355.3968 J
The work done, 'W', on the frictional force on the return of the wagon is given as follows;
W =
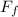 × d₂
× d₂
Where d₂ = the distance moved by the wagon
By conservation of energy, we have;
P.E. = W
∴ 15,355.3968 = 140 × d₂
d₂ = 15,355.4/140 = 109.681405714
Therefore;
The distance the wagon moves from the maximum height, d₂ ≈ 109.68 m
The distance the wagon comes to rest from the starting point, d₃, is given as follows;
d₃ = Horizontal distance + d₁ - d₂
d₃ = 100 m + 21.74 m - 109.68 m ≈ 12.06 m
The distance the wagon comes to rest from the starting point, d₃ ≈ 12.06 m
(c) For the wagon to come finally to rest at it starting point, we have;
The initial kinetic energy = The total work done
1/2·m·v² = 2 ×
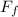 × d
× d
∴ 1/2 × 7,200 × U² = 2 × 140 × d₄
d₄ = 100 + (1/2·m·U² - 140×100)
(1/2·m·U² - 140×100)/(m·g) = h = d₁ × 0.01
∴ d₁ = (1/2·m·U² - 140×100)/(m·g×0.01)
d₄ = 100 + d₁
∴ d₄ = 100 + (1/2·m·U² - 140×100)/(m·g×0.01)
∴ 1/2 × 7,200 × U² = 2 × 140 × (100 + (1/2 × 7,200 × U² - 140×100)/(7,200 × 9.81 ×0.01))
3,600·U² = 280·(100 + (3,600·U² - 14,000)/706.32)
= 28000 + 280×3,600·U²/706.32 - 280 × 14,000/706.32
= 28000 - 280 × 14,000/706.32 + 1427.11518858·U²
3,600·U² - 1427.11518858·U² = 28000 - 280 × 14,000/706.32
U²·(3,600 - 1427.11518858) = (28000 - 280 × 14,000/706.32)
U² = (28000 - 280 × 14,000/706.32)/(3,600 - 1427.11518858) = 10.3319363649
U = √(10.3319363649) = 3.21433295801
The value of 'U' at which the wagon should be propelled if it is to come finally to rest at its starting point is U ≈ 3.214 m/s
Percentage error = (3.214-3.115)/3.214 × 100 ≈ 3.1% < 5% (Acceptable)
The difference in value can come from difference in calculating methods