Question

What would be the answer for this and how?

Answer 1

B. 6 cm

Step-by-step explanation:

First, we calculate the spring constant of a single spring:

`k = (F)/(\Delta x)\\`

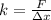
where,

k = spring constant of single spring = ?

F = Force Applied = 10 N

Δx = extension = 4 cm = 0.04 m

Therefore,

`k = (10\ N)/(0.04\ m)\\k = 250\ N/m\\`

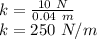
Now, the equivalent resistance of two springs connected in parallel, as shown in the diagram, will be:

`k_(eq) = k + k\\k_(eq) = 2k = 2(250\ N/m)\\k_(eq) = 500\ N/m\\`

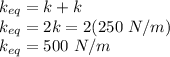
For a load of 30 N, applying Hooke's Law:

`\Delta x = (F)/(k_(eq))\\\\\Delta x = (30\ N)/(500\ N/m)\\\\\Delta x = 0.06\ m = 6\ cm\\`

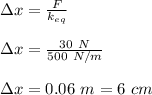
Hence, the correct option is:

B. 6 cm