Question

Ashley and Emma are reading the same article. Ashley is on page 1 of the article, but she can read 1 page per minute. Emma is already on page 5, but reads a page every 3 minutes.

What page is Ashley on after 5 minutes.

What equation can be used to represent the amount Emma has read?

How many minutes does it take before Ashley and Emma have read the same amount

Answer 1

Part A)

Ashley will be on the sixth page.

Part B)

`\displaystyle p=(1)/(3)m+5`

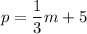
Part C)

Six minutes.

Explanation:

Ashley is on the first page and she can read one page per minute.

Emma is on the fifth page and she can read one page every three minutes.

Part A)

We can write an equation for Ashley. Let m represent the amount of minutes that has passed.

Since she is already one the first page, our initial value is 1.

She reads one page every minute. So, after m minutes, she would have read m pages.

Therefore, our equation is:

`p=m+1`

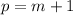
Where p is the total pages read after m minutes.

Then after five minutes, Ashley will be on the:

`p=(5)+1=6`

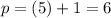
Ashley will be on the sixth page after five minutes.

Part B)

Since Emma reads one page every three minutes, we can say that she reads 1/3 of a page every minute.

Since she started on page five, her equation is:

`\displaystyle p=(1)/(3)m+5`

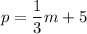
Part C)

So, both of their pages read must be equivalent. Therefore:

`\displaystyle m+1=(1)/(3)m+5`

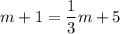
Solve for m. Subtract 1/3m from both sides:

`\displaystyle (2)/(3)m+1=5`

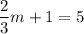
Subtract 1 from both sides:

`\displaystyle (2)/(3)m=4`

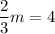
Finally, multiply both sides by 3/2:

`\displaystyle m=4\Big((3)/(2)\Big)=6`

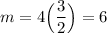
So, it will take six minutes before Ashley and Emma have read the same number of pages.