Question

Carlton and Leon are expert bowlers. Seventy percent of Carlton's rolls are strikes, while 67% of Leon's rolls are strikes. Suppose that Carlton and Leon each bowl 25 games. What is the probability that Leon's proportion of strikes is greater than Carlton's for these games?

Answer 1

The probability that Leon strikes is greater than Carlton strike is 0.40905

Explanation:

From the question, we have;

The percentage of Carlton's rolls are strikes,
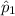`\hat p_1` = 70%

The number of games Carlton played, n₁ = 25

The percentage of Leon's rolls that are strikes,
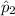`\hat p_2` = 67%

The number of games Leon played, n₂ = 25

Therefore, we have;

`\hat p=(k_1 + k_2)/(n_1 + n_2)`

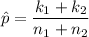
Where;

k₁ = 0.7 × 25 = 17.5

k₂ = 0.67 × 25 = 16.75

`\therefore \hat p=(17.5 + 16.75)/(25 + 25) = 0.685`

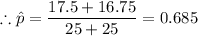
The test statistic is given as follows;

`Z=\frac{\hat{p}_1-\hat{p}_2}{\sqrt{\hat{p} \cdot (1-\hat{p})\cdot \left ((1)/(n_(1))+(1)/(n_(2)) \right )}}`

`Z=\frac{0.7-0.67}{\sqrt{0.685 \cdot (1-0.685)\cdot \left ((1)/(25)+(1)/(25) \right )}} \approx 0.2283`

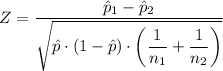
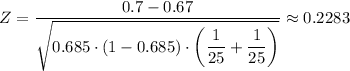
From the z-table, we have;

The p-value for Carlton strikes is greater than Leon's strike = 0.59095

∴ The p-value for Leon strikes is greater than Carlton strike = 1 - 0.59095 = 0.40905

The probability that Leon strikes is greater than Carlton strike = 0.40905