Answer:
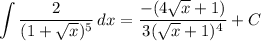
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
- Brackets
- Parenthesis
- Exponents
- Multiplication
- Division
- Addition
- Subtraction
Algebra I
- Exponential Rule [Root Rewrite]:
![\displaystyle \sqrt[n]{x} = x^{(1)/(n)}](https://img.qammunity.org/2022/formulas/mathematics/college/yqpyvbuov0tgbjo8vla0qsqp67pafn2fr7.png)
- Exponential Rule [Rewrite]:
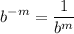
Calculus
Derivatives
Derivative Notation
Basic Power Rule:
- f(x) = cxⁿ
- f’(x) = c·nxⁿ⁻¹
Antiderivatives - Integrals
Integration Constant C
U-Substitution
Integration Rule [Reverse Power Rule]:
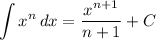
Integration Property [Multiplied Constant]:
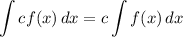
Integration Property [Addition/Subtraction]:
![\displaystyle \int {[f(x) \pm g(x)]} \, dx = \int {f(x)} \, dx \pm \int {g(x)} \, dx](https://img.qammunity.org/2022/formulas/mathematics/high-school/r5yh324r81plt97j3zrr5qi2xxczxlqi34.png)
Explanation:
Step 1: Define
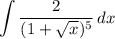
Step 2: Identify Variables
Find the variables u-solve using u-substitution.
U-Substitution
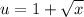
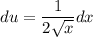
U-Solve
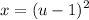
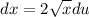
Step 3: Integration
- [Integral] Rewrite [Integration Property - Multiplied Constant]:
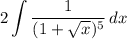
- [Integral] U-Solve:
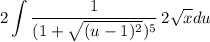
- [Integral] Simplify:
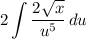
- [Integral] Rewrite [Integration Property - Multiplied Constant]:
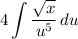
- [Integral] U-Solve:
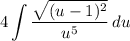
- [Integral] Simplify:
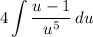
- [Integral] Rewrite [Integration Property - Subtraction]:
![\displaystyle 4[\int {(u)/(u^5)} \, du - \int {(1)/(u^5)} \, du]](https://img.qammunity.org/2022/formulas/mathematics/college/wtjyehrgfywnspzbboipm4p1e2jwu5dmjt.png)
- [Integrals] Simplify:
![\displaystyle 4[\int {(1)/(u^4)} \, du - \int {(1)/(u^5)} \, du]](https://img.qammunity.org/2022/formulas/mathematics/college/u3p0v17g6l9fnfshmx7sf4a25jmnhhqx34.png)
- [Integrals] Rewrite [Exponential Rule - Rewrite]:
![\displaystyle 4[\int {u^(-4)} \, du - \int {u^(-5)} \, du]](https://img.qammunity.org/2022/formulas/mathematics/college/12ggzwp359p9d73ftpd4hbg5bnpz1kh6cd.png)
- [Integrals] Reverse Power Rule:
![\displaystyle 4[(u^(-3))/(-3) - (u^(-4))/(-4)] + C](https://img.qammunity.org/2022/formulas/mathematics/college/dwn0pn6bv35nruuawy463ks223do8ts33m.png)
- Rewrite [Exponential Rule - Rewrite]:
![\displaystyle 4[(-1)/(3u^3) + (1)/(4u^4)] + C](https://img.qammunity.org/2022/formulas/mathematics/college/1jq2ptxyjej8u04t8tzpkkmcdr05u9p4xv.png)
- [Brackets] Multiply:
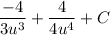
- Back-Substitute:
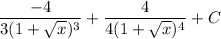
- Combine:
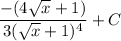
Topic: AP Calculus AB/BC (Calculus I/II)
Unit: Integration
Book: College Calculus 10e