Question

A pump with a power of 5 kW (pump power, and not useful pump power) and an efficiency of 72 percent is used to pump water from a lake to a pool through a constant diameter. The free surface of the pool is 25 m above the free surface of the lake. If the irreversible head loss in the piping system is 4 m, determine (a) the mass flowrate of water and (b) the pressure difference across the pump.

Answer 1

a) The mass flow rate of water is 14.683 kilograms per second.

b) The pressure difference across the pump is 245.175 kilopascals.

Step-by-step explanation:

a) Let suppose that pump works at steady state. The mass flow rate of the water (
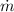`\dot m`), in kilograms per second, is determined by following formula:

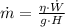`\dot m = (\eta \cdot \dot W)/(g\cdot H)` (1)

Where:

`\dot W` - Pump power, in watts.

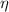`\eta` - Efficiency, no unit.

`g` - Gravitational acceleration, in meters per square second.

`H` - Hydrostatic column, in meters.

If we know that
`\eta = 0.72`,
`\dot W = 5000\,W`,
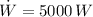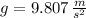`g = 9.807\,(m)/(s^(2))` and
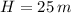`H = 25\,m`, then the mass flow rate of water is:

`\dot m = 14.683\,(kg)/(s)`

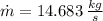
The mass flow rate of water is 14.683 kilograms per second.

b) The pressure difference across the pump (
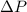`\Delta P`), in pascals, is determined by this equation:

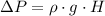`\Delta P = \rho\cdot g\cdot H` (2)

Where
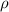`\rho` is the density of water, in kilograms per cubic meter.

If we know that
`\rho = 1000\,(kg)/(m^(3))`,
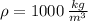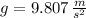`g = 9.807\,(m)/(s^(2))` and
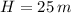`H = 25\,m`, then the pressure difference is:

`\Delta P = 245175\,Pa`

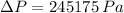
The pressure difference across the pump is 245.175 kilopascals.