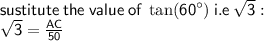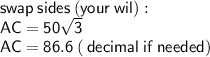Question

Need help with this trigonometry word problem

The angle of elevation of the top of the building at a distance of 50 m from its foot on a horizontal plane is found to be 60°. Find the height of the building.
Please show your work

Answer 1

`\huge \boxed{ \boxed{ 50 √(3) \: or \: 86.6}}`

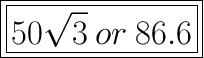
Explanation:

to understand this

you need to know about:

• trigonometry
• PEMDAS

let's solve:

to find the height we need to use tan function because we are given adjacent and angle and we need to figure out opposite (height)
`\tan(\theta)=(opposite)/(adjacent)`

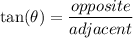
let opposite be AC

let adjacent be BC

according to the question:

`\quad \: \tan( {60}^( \circ) ) = (AC)/(BC)`

now we need a little bit algebra to figure out AC (height)

1. 
   `\sf \: substitute \: the \: given\: value \: of \: BC : \\ \tan( {60}^( \circ) ) = (AC)/(50)`
2. 
   `\sf sustitute \: the \: value \: of \: \tan( {60}^( \circ) ) \: i.e \: √(3) : \\ √(3 ) = (AC )/(50)`
3. 
   `\sf cross \: multiplication: \\ 50 √(3) = AC`
4. 
   `\sf swap \: sides \: (your \: wil) : \\ AC = 50 √(3) \\AC = 86.6 \: ( \sf \: decimal \: if\: needed)`

`\text{we are done!}`