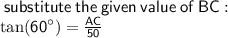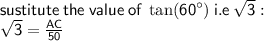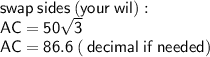Answer:
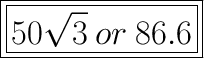
Explanation:
to understand this
you need to know about:
let's solve:
to find the height we need to use tan function because we are given adjacent and angle and we need to figure out opposite (height)
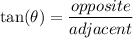
let opposite be AC
let adjacent be BC
according to the question:
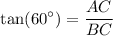
now we need a little bit algebra to figure out AC (height)