Question

Suppose that a wing component on an aircraft is fabricated from an aluminum alloy that has a plane strain fracture toughness of 29 MPa (26.39 ksi). It has been determined that fracture results at a stress of 101 MPa (14650 psi) when the maximum internal crack length is 7.5 mm (0.2953 in.). For this same component and alloy, compute the stress level at which fracture will occur for a critical internal crack length of 5 mm (0.1969 in.).

Answer 1

123.46 MPa

Step-by-step explanation:

( Aluminum alloy Plane strain fracture toughness = 29 MPa ( 26.39 ksi )

Fracture results at a stress of 101 MPa ( psi )

maximum internal crack length = 7.5 mm ( 0.2953 in )

Compute the stress level at which fracture will occur for a critical internal crack length of 5 mm ( 0.1969 in )

Y =
`(KI_(c) )/(\alpha √(\pi a) )`

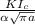
Y = 29 / 101 √π [( 7.5 * 10^-3 ) / 2]

= 29 / 101 √ 0.01178097245 = 29 / ( 101 * 0.1085 )

= 2.65

hence the stress level at which fracture will occur for a critical internal crack length of 5 mm

∝c =
`(KI_(c) )/(y√(\pi a) )`

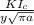
Given; y = 2.65 , KIc = 29, a = ( 5 * 10^-3 ) / 2 = 0.0025

hence ∝c = 29 / 2.65
`√(\pi *0.0025)`

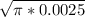
= 29 / 0.2349 ≈ 123.46 MPa