Question

The Medassist Pharmaceutical Company uses a machine to pour cold medicine into bottles in such a way that the standard deviation of the weights is 0.15 oz. A new machine is tested on 71 bottles, and the standard deviation for this sample is 0.12 oz. The Dayton Machine Company, which manufactures the new machine, claims it fills the bottles with less variation. At the 0.05 significance level, test the claim made by the Dayton Machine Company.

Answer 1

hello some part of your question is missing below is the missing part

If Dayton's machine is being used on a trial basis, should its purchase be considered? C.V.(S) = Test Statistic= P-Value= Decision: Conclusion:

answer :

i ) Cv(s) = 51.739

ii) T = 44.8

iii) p-value = 0.0082

iv) we do not fail to reject H0 ( since p-value < 0.05 )

v ) The new machine fills the bottles with a lesser variation

Explanation:

we will test the hypothesis in regards to the standard deviation of the population

The hypothesis are

H0 : б = 0.15

Ha : б < 0.15

hence at ∝ = 0.05 where n = 71

i) critical point for left sided test =
`x^2_(1-\alpha ) , n - 1`

hence Cv(s) = 51.739

ii) Test statistic = T = ( n - 1 ) s^2 / б^2

s = 0.12 , n = 71 , б = 0.15

hence T = 44.8

iii) P-value = p (
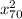`x^(2) _(70)` < 44.8 ) = 0.0082

iv ) Decision : we do not fail to reject H0 ( since p-value < 0.05 )

v ) conclusion : The new machine fills the bottles with a lesser variation