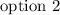Answer:
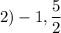
Explanation:
we are given a quadratic equation
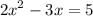
we have to determine the roots
to do so first bring it to standard form i.e
ax²+bx+c=0
move left hand side expression to right hand side and change its sign:
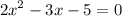
since we moved left hand side expression to right hand side there's only 0 left to the left hand side
we'll use factoring method to solve the quadratic
first, we need to express the middle term as a sum or subtraction of two different terms
to do so
rewrite -3x as 2x-5x:
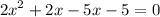
now we have two common factors 2x and -5 so
factor them out:
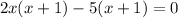
group:
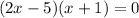
since 2x-5 and x+1 both equal 0
separate the equation as two different equation:
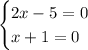
let's work with the first equation:
add 5 to both sides:
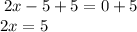
divide both sides by 2:
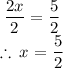
let's work with the second one
cancel 1 from both sides:
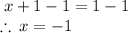
hence,
our answer choice is