Answer:
x = 4
 , y = 8
, y = 8

Explanation:
Using the sine ratio in the right triangle on the left and the exact value
sin45° =
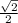
let the altitude of the outer triangle be h ( common to both right triangles )
sin45° =
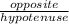 =
=
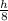 =
=
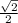 ( cross- multiply )
( cross- multiply )
2h = 8
 ( divide both sides by 2 )
( divide both sides by 2 )
h = 4

----------------------------------------------------------------
Using the tangent ratio in the right triangle on the right and the exact value
tan30° =
 , then
, then
tan30° =
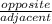 =
=
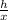 =
=
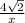 =
=
 ( cross- multiply )
( cross- multiply )
x = 4

--------------------------------------------------------------------
Using the sine ratio in the right triangle on the right and the exact value
sin30° =
 , then
, then
sin30° =
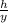 =
=
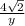 =
=
 ( cross- multiply )
( cross- multiply )
y =8
