Given:
The functions are:
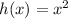

To find:
The transformation from the graph of h to the graph of k.
Solution:
The transformation is defined as
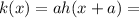 .... (1)
.... (1)
Where, a is stretch factor
If 0<|a|<1, then the graph compressed vertically by factor |a| and if |a|>1, then the graph stretch vertically by factor |a|.
If
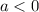 , then the graph of h(x) reflected across the x-axis.
, then the graph of h(x) reflected across the x-axis.
We have,
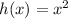

It can be written as
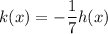 ...(2)
...(2)
On comparing (1) and (2), we get
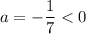
The graph of h(x) reflected across the x-axis.
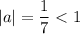
So, the graph is compressed vertically.
It means the graph of h reflection over the x-axls and a vertical stretch to get the graph of k.
Therefore, the correct option is B.