Answer:
a).
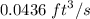 ,
,
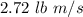
b).
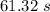
c). 32. ft/s
Step-by-step explanation:
a). The volume flow rate of the water is given by :
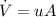
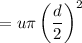
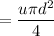


The mass flow rate of the water is given by :


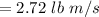
b). The time taken to fill the container is
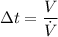
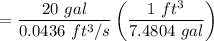
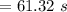
c). The average velocity at the nozzle is :
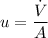
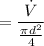
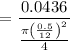
= 32. ft/s