Question

Find f(x) = sin^-1 (2x). Find the value of f'(0)

Answer 1

`\displaystyle f'(0) = 2`

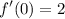
General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Algebra I

• Function
• Function Notation

Pre-Calculus

• Arctrig notation

Calculus

Derivatives

Derivative Notation

Basic Power Rule:

• f(x) = cxⁿ
• f’(x) = c·nxⁿ⁻¹

Derivative Rule [Chain Rule]:
`\displaystyle (d)/(dx)[f(g(x))] =f'(g(x)) \cdot g'(x)`

Arctrig Derivative:
`\displaystyle (d)/(dx)[arcsinu] = (u')/(√(1 - u^2))`

Explanation:

Step 1: Define

`\displaystyle f(x) = sin^(-1)(2x)`

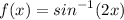
f'(0) is x = 0 for the 1st derivative function

Step 2: Differentiate

1. [Derivative] Arctrig Derivative [Derivative Rule - Chain Rule]:
   `\displaystyle f'(x) = ((d)/(dx)[2x])/(√(1 - (2x)^2))`
2. [Derivative] Basic Power Rule:
   `\displaystyle f'(x) = (1 \cdot 2x^(1 - 1))/(√(1 - (2x)^2))`
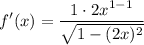
3. [Derivative] Simplify:
   `\displaystyle f'(x) = (2)/(√(1 - 4x^2))`

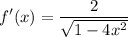
Step 3: Evaluate

1. Substitute in x [Derivative]:
   `\displaystyle f'(0) = (2)/(√(1 - 4(0)^2))`
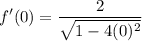
2. [√Radical] Exponents:
   `\displaystyle f'(0) = (2)/(√(1 - 4(0)))`
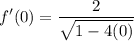
3. [√Radical] Multiply:
   `\displaystyle f'(0) = (2)/(√(1))`
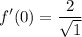
4. [Fraction] Square Root:
   `\displaystyle f'(0) = (2)/(1)`
5. [Fraction] Division:
   `\displaystyle f'(0) = 2`

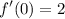
Topic: AP Calculus AB/BC (Calculus I/II)

Unit: Integration - Special Functions (Arctrig)

Book: College Calculus 10e