Answer:
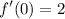
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
- Brackets
- Parenthesis
- Exponents
- Multiplication
- Division
- Addition
- Subtraction
Algebra I
- Function
- Function Notation
Pre-Calculus
Calculus
Derivatives
Derivative Notation
Basic Power Rule:
- f(x) = cxⁿ
- f’(x) = c·nxⁿ⁻¹
Derivative Rule [Chain Rule]:
![\displaystyle (d)/(dx)[f(g(x))] =f'(g(x)) \cdot g'(x)](https://img.qammunity.org/2022/formulas/mathematics/high-school/vue68srn3fe6bds4idxorm97z7tgwelamw.png)
Arctrig Derivative:
![\displaystyle (d)/(dx)[arcsinu] = (u')/(√(1 - u^2))](https://img.qammunity.org/2022/formulas/mathematics/college/zi8ha9469ngmomto9iqu4hiqktji6dyrcb.png)
Explanation:
Step 1: Define
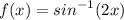
f'(0) is x = 0 for the 1st derivative function
Step 2: Differentiate
- [Derivative] Arctrig Derivative [Derivative Rule - Chain Rule]:
![\displaystyle f'(x) = ((d)/(dx)[2x])/(√(1 - (2x)^2))](https://img.qammunity.org/2022/formulas/mathematics/college/hyakucztoozg842hgftbvcopgbg3vhtbxg.png)
- [Derivative] Basic Power Rule:
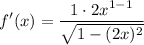
- [Derivative] Simplify:
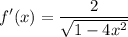
Step 3: Evaluate
- Substitute in x [Derivative]:
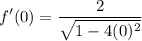
- [√Radical] Exponents:
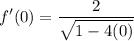
- [√Radical] Multiply:
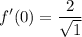
- [Fraction] Square Root:
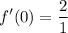
- [Fraction] Division:
Topic: AP Calculus AB/BC (Calculus I/II)
Unit: Integration - Special Functions (Arctrig)
Book: College Calculus 10e