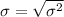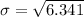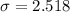Question

The data in this question will be utilized for the next three questions. The number of pets a group of students have are given below.Solute deviation?

Answer 1

Question

The data in this question will be utilized for the next three questions. The number of pets a group of students has, are given below.

Number of pets: 0-2 2-4 4-6 6-8 8-10 10-12 12-14

Number of students: 1 2 1 5 6 2 3

Calculate

(1) Mean (2) Sample Variance (3) Sample Standard Deviation

Answer:

`(1)`
`\bar x = 8.1`

`(2)`
`\sigma^2 = 6.341`

`(3)`
`\sigma = 2.518`

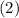
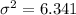
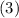
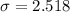
Explanation:

Given

The above data

First, we calculate the class midpoint (x)

Pets:
`0-2`
`2-4`
`4-6`
`6-8`
`8-10`
`10-12`
`12-14`

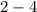
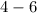
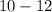
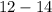
x 1 3 5 7 9 11 13

f: 1 2 1 5 6 2 3

The class midpoint (x) is calculated by the average of each group.

For pets: 0 - 2.

`x = (0 + 2)/(2)= (2)/(2) = 1`

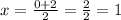
The same is done for other groups.

Solving (a): Mean

`\bar x = (\sum fx)/(\sum f)`

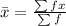
This gives:

`\bar x = (1 * 1 + 3 * 2 + 5 * 1 + 7 * 5 + 9 * 6 + 11 * 2 + 13 * 3)/(1 + 2 + 1 + 5 + 6 + 2 + 3)`

`\bar x = (162)/(20)`

`\bar x = 8.1`

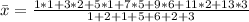
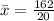
Solving (b): Sample Variance

This is calculated as:

`\sigma^2 = (\sum(x_i - \bar x)^2)/(\sum f - 1)`

So:

`\sigma^2 = ((1 - 8.1)^2+(3 - 8.1)^2+(5 - 8.1)^2+(7 - 8.1)^2+(9 - 8.1)^2+(11 - 8.1)^2+(13 - 8.1)^2)/(20 - 1)`

`\sigma^2 = (120.47)/(19)`

`\sigma^2 = 6.341`

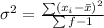
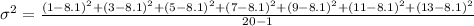
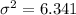
Solving (c): The sample standard deviation

This is calculated as:

`\sigma = \sqrt{\sigma^2`

`\sigma = \sqrt{6.341`

`\sigma = 2.518`