Question

A recent newspaper article claimed that more people read Magazine A than read Magazine B. To test the claim, a study was conducted by a publishing representative in which newsstand operators were selected at random and asked how many of each magazine were sold that day. The representative will conduct a hypothesis test to test whether the mean number of magazines of type A the operators sell, μAμA, is greater than the mean number of magazines of type B the operators sell, μBμB. What are the correct null and alternative hypotheses for the test?

A. H0:μA−μB=0Ha:μA−μB>0H0:μA−μB=0Ha:μA−μB>0
B. H0:μA−μB<0Ha:μA−μB>0H0:μA−μB<0Ha:μA−μB>0
C. H0:μA−μB=0Ha:μA−μB≠0H0:μA−μB=0Ha:μA−μB≠0
D. H0:x¯A−x¯B=0Ha:x¯A−x¯B>0H0:x¯A−x¯B=0Ha:x¯A−x¯B>0
E. H0:μB−μA=0Ha:μB−μA>0H0:μB−μA=0Ha:μB−μA>0

Answer 1

Option A.

Explanation:

The representative will conduct a hypothesis test to test whether the mean number of magazines of type A the operators sell, μAμA, is greater than the mean number of magazines of type B the operators sell, μBμB. What are the correct null and alternative hypotheses for the test?

To verify this, the distribution used is
`\mu_(A) - \mu_(B)`

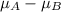
The null hypothesis is an equality, which means that it is:

`H_(0) = \mu_(A) - \mu_(B) = 0`

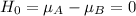
At the alternate hypothesis, we want to test if the mean number of type A is greater than type B, that is, the distribution is positive. So

`H_(A) = \mu_(A) - \mu_(B) > 0`

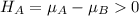
So the correct answer is given by option A.