Answer:
h = 40.37 m
Step-by-step explanation:
We will apply the law of conservation of energy to the skier in this case, as follows:
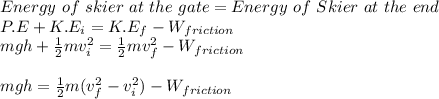
where,
m = mass of skier = 77 kg
g = acceleration due to gravity = 9.81 m/s²
vf = final speed = 30 m/s
vi = initial speed = 2 m/s
W_friction = Work done by friction and air resistance = 4000 J
Therefore,
![(77\ kg)(9.81\ m/s^2)h = (1)/(2)(77\ kg)[(30\ m/s)^2-(2\ m/s)^2] - 4000\ J\\\\h = (34496\ J - 4000\ J)/(755.37\ N)\\\\](https://img.qammunity.org/2022/formulas/physics/college/nwcyzh7fg6hc2ax8gmk93yg99ppaqu64b0.png)
h = 40.37 m