Question

You are designing a ski jump ramp for the next Winter Olympics. You need to calculate the vertical height h from the starting gate to the bottom of the ramp. The skiers push off hard with their ski poles at the start, just above the starting gate, so they typically have a speed of 2.0 m/s as they reach the gate. For safety, the skiers should have a speed of no more than 30.0 m/s when they reach the bottom of the ramp. You determine that for a 77.0 kg skier with good form, friction and air resistance will do total work of magnitude 4000 J on him during his run down the slope.

Required:
What is the maximum height h for which the maximum safe speed will not be exceeded?

Answer 1

h = 40.37 m

Step-by-step explanation:

We will apply the law of conservation of energy to the skier in this case, as follows:

`Energy\ of\ skier\ at\ the\ gate = Energy\ of\ Skier\ at\ the\ end\\P.E + K.E_(i) = K.E_(f) - W_(friction)\\mgh + (1)/(2)mv_(i)^2 = (1)/(2)mv_(f)^2 - W_(friction)\\\\mgh = (1)/(2)m(v_(f)^2-v_(i)^2) - W_(friction)`

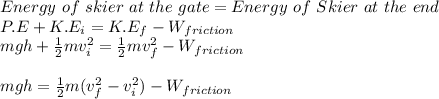
where,

m = mass of skier = 77 kg

g = acceleration due to gravity = 9.81 m/s²

vf = final speed = 30 m/s

vi = initial speed = 2 m/s

W_friction = Work done by friction and air resistance = 4000 J

Therefore,

`(77\ kg)(9.81\ m/s^2)h = (1)/(2)(77\ kg)[(30\ m/s)^2-(2\ m/s)^2] - 4000\ J\\\\h = (34496\ J - 4000\ J)/(755.37\ N)\\\\`

h = 40.37 m