Answer:
2.75units
Explanation:
Find the diagram attached
The length of an arc is expressed as shown;
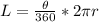
r is the radius = length of GH
r = GH = 11units
m<GHJ = 34 degree
Substitute the given parameters into the equation given;
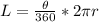
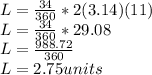
Hence the length of the arc to the nearest hundredth is 2.75units