Question

The roof of a clock tower is a square pyramid. Each side of the base is 16ft long. The slant height is 22ft. What is the lateral area of the roof?

Answer 1

The area of the pyramid is 703.97 ft²

Explanation:

The lateral area of a right square pyramid is given as;

`A_l =a √(a^2 + 4h^2)`

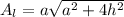
where;

a is base length

h is the vertical height of the pyramid

The vertical height of the pyramid is calculated as follows;

the vertical height passes through the center of the base.

half of the base = 8 ft

the slant height = hypotenuse side of the right triangle = 22 ft

Thus; h² = 22² - 8²

h² = 420

h = √420

h = 20.493 ft

The area of the pyramid is calculated as;

`A_l =a √(a^2 + 4h^2)\\\\A_l =16√(16^2 + 4(20.493)^2) \\\\A_l = 703.97 \ ft^2`

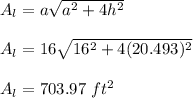
Therefore, the area of the pyramid is 703.97 ft²