Answer:
We should use the following transformation:
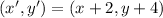 (Translation of circle A to the center of the circle B)
(Translation of circle A to the center of the circle B)
Explanation:
We should apply a translation prior to determine if both circles are similar. If we translate the circle A to the center of the circle B. The translation needed is the vectorial distance between both centers:
 (1)
(1)
Where:
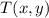 - Translation vector.
- Translation vector.
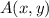 - Location of the center of the circle A.
- Location of the center of the circle A.
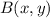 - Location of the center of the circle B.
- Location of the center of the circle B.
If we know that
 and
and
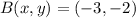 , then the translation vector is:
, then the translation vector is:
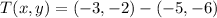
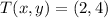
We should use the following transformation:
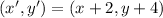 (Translation of circle A to the center of the circle B)
(Translation of circle A to the center of the circle B)