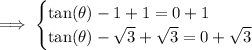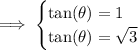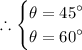Answer:
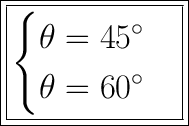
Explanation:
to understand this
you need to know about:
let's solve:
distribute tan(θ):
=>tan²(θ)-(tan(θ)+√3tan(θ))+√3=0
remove parentheses:
=>tan²(θ)-tan(θ)-√3tan(θ)+√3=0
so this equation is now in standard form i.e ax²+bx+c=0
we can solve by factoring as we solve quadratic equation
factor out tanθ:
=>tan(θ)(tan(θ)-1)-√3tan(θ)+√3=0
factor out -√3:
=>tan(θ)(tan(θ)-1)-√3(tan(θ)-1)=0
group:
=>(tan(θ)-√3)(tan(θ)-1)=0
separate it as two different equation:
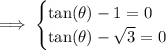
add 1 and √3 to both sides to first and second equation respectively: