Answer:
Explanation:
1). By the theorem for the length of the segments of the intersecting chords in a circle,
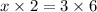
x = 9
2). By the theorem of secants intersecting outside a circle,
4 × 9 = x × 12
x =
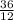
x = 3
3). By the theorem of secant and tangent intersecting outside a circle,
x² = 2(2 + 6)
x² = 16
4). By the theorem of secant and tangent intersecting outside a circle,
6² = 3x
3x = 36
x = 12
5). By the theorem for the length of the segments of the intersecting chords in a circle,
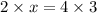
x = 6