Answer:
a) The maximum flowrate of the pump is approximately 13,305.22 cm³/s
b) The pressure difference across the pump is approximately 293.118 kPa
Step-by-step explanation:
The efficiency of the pump = 78%
The power of the pump = 5 -kW
The height of the pool above the underground water, h = 30 m
The diameter of the pipe on the intake side = 7 cm
The diameter of the pipe on the discharge side = 5 cm
a) The maximum flowrate of the pump is given as follows;
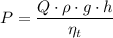
Where;
P = The power of the pump
Q = The flowrate of the pump
ρ = The density of the fluid = 997 kg/m³
h = The head of the pump = 30 m
g = The acceleration due to gravity ≈ 9.8 m/s²
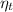 = The efficiency of the pump = 78%
= The efficiency of the pump = 78%
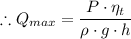
 = 5,000 × 0.78/(997 × 9.8 × 30) ≈ 0.0133 m³/s
= 5,000 × 0.78/(997 × 9.8 × 30) ≈ 0.0133 m³/s
The maximum flowrate of the pump
 ≈ 0.013305 m³/s = 13,305.22 cm³/s
≈ 0.013305 m³/s = 13,305.22 cm³/s
b) The pressure difference across the pump, ΔP = ρ·g·h
∴ ΔP = 997 kg/m³ × 9.8 m/s² × 30 m = 293.118 kPa
The pressure difference across the pump, ΔP ≈ 293.118 kPa