Answer:
The sample size is 1875.
Explanation:
In a sample with a number n of people surveyed with a probability of a success of
 , and a confidence level of
, and a confidence level of
 , we have the following confidence interval of proportions.
, we have the following confidence interval of proportions.

In which
z is the zscore that has a pvalue of
 .
.
The margin of error is:

Sampling error of 0.03.
This means that
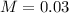
99.74% confidence level
So
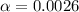 , z is the value of Z that has a pvalue of
, z is the value of Z that has a pvalue of
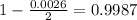 , so
, so
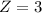 .
.
25% of all adults had used the Internet for such a purpose
This means that
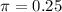
What is the sample size
The sample size is n. So

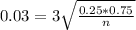
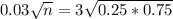
Simplifying by 0.03 both sides
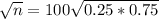
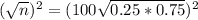
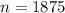
The sample size is 1875.