Question

A charged, parallel-plate capacitor is isolated. If the distance separating the plates of the capacitor decreases to half the original distance, what happens to the magnitude of the electric field between the two plates?

Answer 1

Hi there!

Recall the following:

`C = (Q)/(V)`

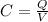
C = Capacitance (F)
Q = Charge (C)
V = Potential difference (V)

The equation for the capacitance of a parallel-plate capacitor:

`C = (\epsilon_0 A)/(d)`

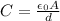
C = Capacitance (F)
ε₀ = Permittivity of Free Space

A = Area of plates (m²)
d = distance between plates (m)

If the distance is halved, the capacitance will DOUBLE since there is an inverse relationship between capacitance and distance.

Thus, something has to change in regards to the charge or voltage for it to match the doubled capacitance.

Since the capacitor is ISOLATED, it is not connected to a battery, so the voltage is NOT maintained constant. The VOLTAGE will consequentially be changed, while the electric field will be unchanged.

Recall the equation for potential difference:

`V = Ed`

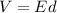
If the distance is halved, the voltage will be halved. This is mirrored by the doubled capacitance. Thus, the electric field will remain the SAME.