Question

An 1120 kg car traveling at 17 m/s is brought to a stop while skidding 40 m. Calculate the work done on the car by friction forces.

Answer 1

Approximately
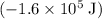`(-1.6 * 10^(5)\; \rm J)` (assuming that the car was on level ground.)

Step-by-step explanation:

When an object of mass
`m` is moving at a speed of
`v`, the kinetic energy of that object would be
`(1/2) \, m \cdot v^(2)`.

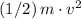Initial kinetic energy of the car:

`\begin{aligned}&(1)/(2)\, m \cdot v^(2) \\ &= (1)/(2)* 1120\; \rm kg * (17\; \rm m \cdot s^(-1))^(2) \\ &\approx 1.6* 10^(5)\; \rm J \end{aligned}`.

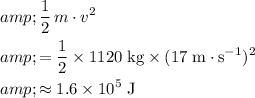After the car comes to a stop, the kinetic energy of this car would be
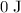`0\; \rm J` because the car would not be moving.

Change to the kinetic energy of the car:
`\text{Final KE} - \text{Initial KE} = -1.6 * 10^(5)\; \rm J`.

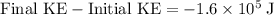If the car is traveling on level ground, friction would be the only force that contributed to this energy change. Hence:

`\text{Work of friction} = \text{Energy change} = -1.6* 10^(5)\; \rm J`.

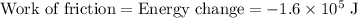The value of the work that friction did is negative. The reason is that at any instant before the car comes to a stop, friction would be exactly opposite to the direction of the movement of the car.

The work of a force on an object is the dot product of that force and the displacement of that object. The dot product of two vectors of opposite directions is negative. Hence, in this question, the work that friction did on the car would be negative because the friction vector would be opposite to the movement of the car.