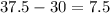Hi there!
a.
We can find the x-coordinate by deriving an expression for the line and arc, then setting the two equal.
We are given that the graph has the equation:
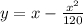
Differentiate to solve for the slope:

This is the slope of the line at 'p'. We are given that the line passes through (-15, 0), so we can use the point-slope formula:
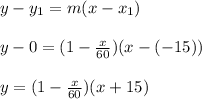
Since this line intersects at 'p', we can set this equation along with the equation for the arc equal to each other to solve for 'x'.
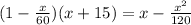
Solve using a graphing utility.
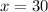
b.
We can write an equation for line 'l' by solving for the slope at the 'p' value.
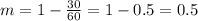
Now, use the point-slope formula with this y-value and the x-axis intersection coordinates.
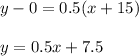
c.
We can plug x = 60 into both function equations to find the distance.
For the arc:
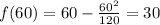
For the line:
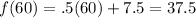
Subtract to find the distance. (QR)