Answer:
The terms of the sequence are x=5 and a=2:
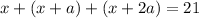 →
→
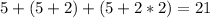
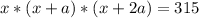 →
→
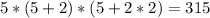
Explanation:
We can find the terms of the following sequence:
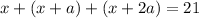
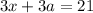
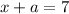 (1)
(1)
The product of that sequence is:
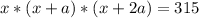 (2)
(2)
Solving equation (1) for x:
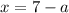 (3)
(3)
And by entering (3) into (2):
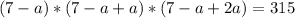
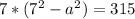
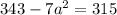

Now, by entering "a" into equation (3):

Therefore, the terms of the sequence are x=5 and a=2.
I hope it helps you!