Question

Please help me with 6-7 / 10 points

Answer 1

6) Axis of symmetry x=1. Vertex at (5,1)

7) Axis of symmetry x=1. Vertex at (1,2). y-intercept at y = -1

Explanation:

There is an equation to find the axis of symmetry of a quadratic function and is given by:

Knowing that the standard form of a quadratic equation is:

`y=ax^(2)+bx+c`

The axis of symmetry is:

`x=(-b)/(2a)` (1)

(6)

The quadratic equation of the first problem is:

`y=2x^(2)-4x+7`

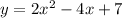
Then, using equation (1) the axis of symmetry will be:

`x=(-(-4))/(2(2))`

`x=(4))/(4)`

`x=1`

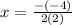
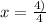
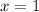
We need to use this value of x to find the vertex;

`y(1)=2(1)^(2)-4(1)+7`

`y(1)=5`

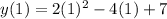
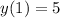
The vertex is (5,1)

Therefore, we disagree with Ahmed. The axis of symmetry is x = 1 and the vertex is in the point (5,1).

(7)

We can use the same method here. The function is:

`f(x)=-3x^(2)+6x-1`

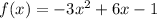
The axis of symmetry is:

`x=(-6)/(2(-3))`

`x=1`

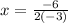
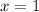
The vertex is:

`f(1)=-3(1)^(2)+6(1)-1`

`f(1)=2`

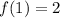
So the vertex is (1,2)

We need to evaluate the function at x = 0 to get the y-intercept value.

`f(0)=-3(0)^(2)+6(0)-1`

`f(0)=-1`

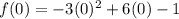
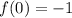
Therefore, the y-intercept is at y = -1.

I hope it helps you!