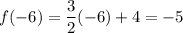Answer:
D (-6, -5)
Explanation:
We need to create a linear function for the set of coordinates, input the x-values of the possible options into the function, then see which one gives the correct y-value.
Pick 2 coordinate pairs from the set:
Let
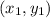 = (0, 4)
= (0, 4)
Let
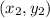 = (-2, 1)
= (-2, 1)
Use slope formula:
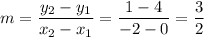
Use equation of a line in point-slope form to create the linear function:
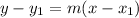
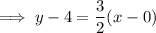
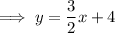
Therefore, the linear function is
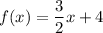
Inputting the x-values of the possible options, (-6, -5) is the only coordinate pair that is correct: