Answer:
Explanation:
Let the equation of the line 'a' is,
y = mx + c
Here, m = slope of the line
c = y-intercept
For line 'a',
Slope of the line =
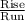
m =
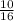
m =

y-intercept = 20
Therefore, equation of the line 'a' is,
y =
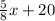
Similarly, equation of the line 'b' is,
y = m'x + c'
Slope of the line =
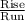
m' =
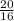
m' =
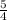
y-intercept = 0
Therefore, equation of the line is 'b' is,
y =
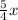
1). Line 'b' represents a proportional relationship → FALSE
2). The constant of proportionality of y to x for line 'a' is
 → FALSE
→ FALSE
3). The ratio of y-coordinate to x-coordinate of one of the points on line b is 25 : 8 → FALSE
4). let a passes through the point
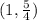 so the constant of proportionality is
so the constant of proportionality is
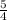 → TRUE
→ TRUE