Question

I'm awarding 20 points for an answer!

A ball is thrown into the air with an initial upward velocity of 48 ft/s. It height h in feet after t seconds is given by the function h (t)=-16t^2+48t+4.

What is the ball's maximum height?

Answer 1

40 feet (after 1.5 seconds).

Explanation:

The height h of the ball after t seconds is modeled by the function:

`h(t)=-16t^2+48t+4`

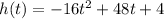
And we want to determine the ball's maximum height.

Since the given function is a quadratic, the maximum height occurs at the vertex point.

For quadratics, the vertex point is given by the formulas:

`\displaystyle \Big(-(b)/(2a),f\Big(-(b)/(2a)\Big)\Big)`

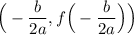
In this case, a = -16, b = 48, and c = 4.

Therefore, the t-coordinate at which the vertex occurs is:

`\displaystyle t=-(48)/(2(-16))=(48)/(32)=(3)/(2)`

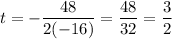
So, the maximum height occurs after 1.5 seconds.

Then the maximum height will be:

`\begin{aligned}\displaystyle h\Big((3)/(2)\Big)&=-16\Big((3)/(2)\Big)^2+48\Big((3)/(2)\Big)+4\\\\ &=-16\Big((9)/(4)\Big)+24(3)+4\\\\&=-4(9)+72+4\\\\&=40\text{ feet}\end{aligned}`

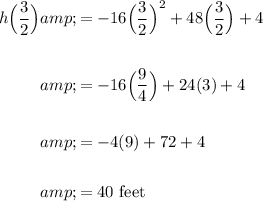
So, the maximum of the ball is 40 feet (after 1.5 seconds).