Question

Please simplify the following trigonometric identity.


`\displaystyle(1)/(\sec\alpha-\tan\alpha)`

Answer 1

cos a

---------------------

1 -sin (a)

Explanation:

We know that sec a = 1/ cos (a) and tan a = sin (a) / cos (a)

1

---------------------

1/ cos (a) -sin (a) / cos (a)

Multiply the top and bottom by cos (a)

1* cos a

---------------------

( 1/ cos (a) -sin (a) / cos (a)) * cos a

cos a

---------------------

1 -sin (a)

Answer 2

Examining the question:

We are given the expression:

`(1)/(Sec(\alpha)-Tan(\alpha))`

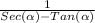
We know from Basic trigonometry that:

`Sec(\alpha) = (1)/(Cos(\alpha))`

`Tan(\alpha) = (Sin(\alpha))/(Cos(\alpha))`

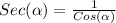
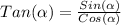
Simplifying the expression:

Replacing these values in the given expression, we get:

`(1)/((1)/(Cos(\alpha)) -(Sin(\alpha))/(Cos(\alpha)) )`

Since the denominator of both the values in the denominator is the same:

`(1)/((1-Sin(\alpha))/(Cos(\alpha)) )`

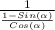
We know that
`(1)/((a)/(b) )` =
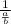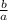`(b)/(a)`, using the same property:

`(Cos(\alpha))/(1-Sin(\alpha))`

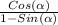
and we are done!