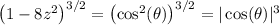Question

Hello everyone, I'm just having trouble on two questions for my Calculus work. I need to solve them using trig substitution to eliminate the root. Does anyone know where to start with this problem? Any help would be greatly appreciated!

Answer 1

The main idea is to exploit the trigonometric identity,

sin²(θ) + cos²(θ) = 1

2. For an integral containing 16 - 81x², you might substitute x = 4/9 sin(θ) (with differential dx = 4/9 cos(θ) dθ, but without an actual integral to work with this isn't really important). Then

16 - 81x² = 16 - 81 (4/9 sin(θ))²

… = 16 - 81 (16/81 sin²(θ))

… = 16 - 16 sin²(θ)

… = 16 (1 - sin²(θ))

… = 16 cos²(θ)

so that in the root expression, we would end up with

`\left(16 - 81x^2\right)^(7/2) = \left(16\cos^2(\theta)\right)^(7/2) = 2^(14) |\cos(\theta)|^7`

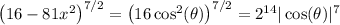
since
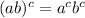`(ab)^c=a^cb^c` for all real a, b, and c;
`16^(7/2)=\left(2^4\right)^(7/2)=2^(14)`; and
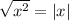`√(x^2)=|x|` for all real x.

The goal is to replace x with some multiple of sin(θ) that makes the coefficients factor out like they did here, which then lets you reduce 1 - sin²(θ) to cos²(θ).

And don't be discouraged by the absolute values; in the context of a definite integral, there are things that can be done to remove them or otherwise simplify absolute value expressions.

3. Substitute z = 1/√8 sin(θ) (so that dz = 1/√8 cos(θ) dθ). Then

1 - 8z² = 1 - 8 (1/√8 sin(θ))²

… = 1 - 8 (1/8 sin²(θ))

… = 1 - sin²(θ)

… = cos²(θ)

so that

`\left(1-8z^2\right)^(3/2) = \left(\cos^2(\theta)\right)^(3/2) = |\cos(\theta)|^3`