Question

Using what you know about right triangle trigonometry, salt the triangle round the side to the nearest 10th and angle measures to the nearest degree.

PLEASE provide an explanation in your response :)

Answer 1

Angle A = 49° Angle B = 41° Side AB = 30.5

Explanation:

Let's work out Angle A and Angle B first. We are given AC and CB, therefore AB must be the hypotenuse as it is the longest side.

AC and CB must be the opposite and adjacent sides, therefore we can use tan(x) = Opposite/Adjacent for working out both Angle A and Angle B.

Angle A:

tan(A) = 23/20 For Angle A, CB (23) is the side opposite the angle and AC (20) is the side in between Angle A and the right angle, also the adjacent side.

A =
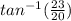`tan^(-1)((23)/(20))` We do the inverse of tan here.

A = 48.9909131

A = 49° Rounding to the nearest degree simply means to the nearest whole number.

Angle B:

tan(B) = 20/23 For Angle B, AC (20) is the side opposite the angle and CB (23) is the side in between Angle B and the right angle, also the adjacent side.

B =
`tan^(-1)((20)/(23))`

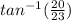
B = 41.0090869

B = 41°

Side AB:

We can just use Pythagoras' Theorem here to work out AB, but I will also use trigonometry to show you how you can use both formulas. When I use trigonometry, I will only be using Angle A as an example.

Pythagoras' Theorem:
`a^(2) + b^(2) = c^(2)`

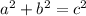
AC = 20 = a

CB = 23 = b

`20^(2) + 23^(2) = c^(2)`

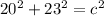
929 =
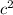
`c^(2)`

c =
`√(929)`

c = 30.47950131

c = 30.5 Rounding to the nearest 10th simply means rounding to 1 decimal place.

Trigonometry: SOHCAHTOA

Angle A = 49°

AC = 20 I will use AC as our adjacent side instead of CB. They will both give us the same answer anyways.

AB will always be the hypotenuse in the given right-angled triangle.

cos(x) = Adjacent/Hypotenuse

cos(49) = 20/AB

ABcos(49) = 20 Here we multiply by AB, our hypotenuse.

AB = 20/cos(49) Now we divide by cos(49)

AB = 30.48506173 As you can see here, this answer is different from the Pythagoras' Theorem one because we rounded our angle values, meaning out angle values aren't exact! Instead, use Pythagoras' Theorem here for more accurate results instead of Trigonometry.

AB = 30.5 They still give us the same answer in the end!

I hope this helps you!! ^-^