Answer:
If all these three charges are positive with a magnitude of
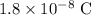 each, the electric potential at the midpoint of segment
each, the electric potential at the midpoint of segment
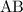 would be approximately
would be approximately
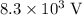 .
.
Step-by-step explanation:
Convert the unit of the length of each side of this triangle to meters:
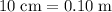 .
.
Distance between the midpoint of
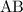 and each of the three charges:
and each of the three charges:
Let
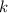 denote Coulomb's constant (
denote Coulomb's constant (
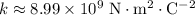 .)
.)
Electric potential due to the charge at
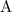 :
:
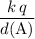 .
.
Electric potential due to the charge at
 :
:
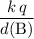 .
.
Electric potential due to the charge at
 :
:
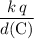 .
.
While forces are vectors, electric potentials are scalars. When more than one electric fields are superposed over one another, the resultant electric potential at some point would be the scalar sum of the electric potential at that position due to each of these fields.
Hence, the electric field at the midpoint of
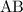 due to all these three charges would be:
due to all these three charges would be:
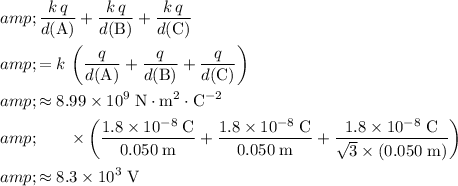 .
.