Question

The settlement analysis for a proposed structure indicates that the underlying clay layer will settle 7.5 cm in 3 years, and that ultimately the total settlement will be about 32 cm. However, this analysis is based on the clay layer being doubly drained. It is suspected that there may be no drainage at the bottom of the layer (i.e., clay has single drainage condition). Answer the following questions based on single drainage only, assuming cv = 1.5 x 10-4 cm 2 /s for both single and double drainage.

a. How will the total settlement change from the double to the single drainage case?
b. How long will it take for 7.5 cm of settlement to occur if there is only single

Answer 1

A) For a double drainage system the time taken for total settlement will differ from that of a single drainage system, because in a double drainage case clay water escapes from both sides unlike in a single drainage case. hence water and air will be be expulsed faster for a double drainage making it attain total settlement faster.

B) for only single = 12 years

Step-by-step explanation:

Given data :

ultimate clay settlement = 32 cm

settlement of clay in 3 years = 7.5 cm

Cv ( coefficient of consolidation ) = 1.5 x 10^-4 cm^2 /s

A) For a double drainage system the time taken for total settlement will differ from that of a single drainage system, because in a double drainage case clay water escapes from both sides unlike in a single drainage case. hence water and air will be be expulsed faster for a double drainage making it attain total settlement faster.

note : Total settlement is the same in both drainage system.

B) Determine how long it will take for 7.5 cm of settlement to occur if there is only single

applying the relation below

Tv = Cv t / H^2

where Tv = time factor , d = thickness of layer , H = drainage path

Given that Tv and Cv are constant in both cases

t ∝ H^2 hence

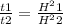`(t1)/(t2) = (H^21)/(H^22)` ------ ( 1 )

t1 = time for single drainage for d meters , t2 = time for double drainage for d meters

equation 1 can be rewritten as

t1/t2 = d^2 / (d/2)^2

∴ t1 = 4t2

given that t2 = 3 years ( value gotten from question )

t1 = 4 * 3 = 12 years