Answer:
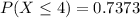
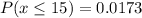
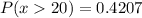
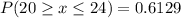

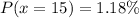
Step-by-step explanation:
Given
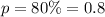
The question illustrates binomial distribution and will be solved using:
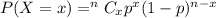
Solving (a):
Given

Required
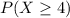
This is calculated using
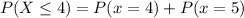
This gives:
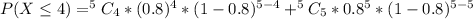

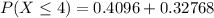
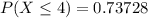
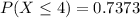 --- approximated
--- approximated
Solving (b):
Given

i)
Required
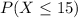
This is calculated as:
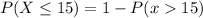 --- Complement rule
--- Complement rule
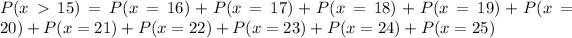
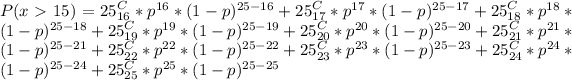
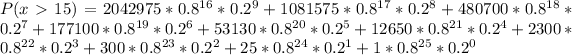
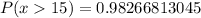
So:
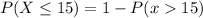

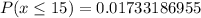
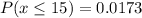
ii)
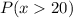
This is calculated as:


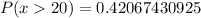
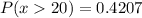
iii)
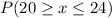
This is calculated as:
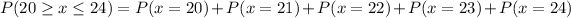
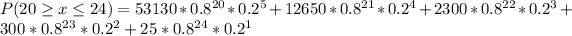
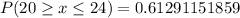
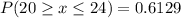
iv)
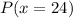
This is calculated as:


Solving (c):

This is calculated as:
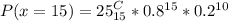
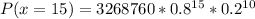
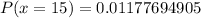
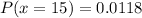
Express as percentage
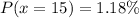
The calculated probability (1.18%) is way less than the advocate's claim.
Hence, we do not believe the claim.