Question

On the Apollo 14 mission to the moon, astronaut Alan Shepard hit a golf ball with a golf club improvised from a tool. The free-fall acceleration on the moon is 1/6 of its value on earth. Suppose he hit the ball with a speed of 25 m/s at an angle 30 ^ { \circ }30

∘
above the horizontal. a. How long was the ball in flight? b. How far did it travel? c. Ignoring air resistance, how much farther would it travel on the moon than on earth?

In cases like these(when calculating the projectile motion), when do I add a negative sign in front of ay (9.8, the free fall acceleration) or do i always need a negative sign in front of ay

Answer 1

a. The ball would have been in flight for approximately
`15.3\; {\rm s}`.

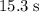b. The range of the ball would be approximately
`3.31 * 10^(2)\; {\rm m}`.

c. The ball would have travelled approximately
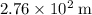`2.76 * 10^(2)\; {\rm m}` further than it would have travelled on the earth.

In a projectile motion, quantities such as acceleration and velocity are vectors. By convention, if a vector quantity is one-dimensional in the vertical direction (e.g., vertical velocity,) that quantity should be greater than zero (no negative sign) if it points upwards and negative otherwise.

Step-by-step explanation:

The question states that the initial velocity of this ball is
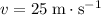`v = 25\; {\rm m \cdot s^(-1)}` and points upwards with an elevation angle of
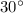`30^(\circ)`. Decompose this velocity into horizontal and vertical components:

Horizontal component:

`\begin{aligned}v_(x) &= v\, \cos(30^(\circ)) \\ &= 25\; {\rm m \cdot s^(-1)} * \cos(30^(\circ)) \\ &\approx 21.651\; {\rm m\cdot s^(-1)}\end{aligned}`.

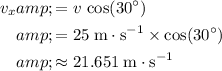Vertical component:

`\begin{aligned}v_(y) &= v\, \sin(30^(\circ)) \\ &= 25\; {\rm m \cdot s^(-1)} * \sin(30^(\circ)) \\ &= 12.5\; {\rm m\cdot s^(-1)}\end{aligned}`.

If the air resistance on the ball is negligible, the mechanical energy of the ball would be conserved. Thus, the kinetic energy of the ball would be the same at launch and right before the ball lands.

The magnitude of the vertical velocity of the ball would be the same at launch and right before landing, but the direction would be the exact opposite. The initial vertical velocity of the ball would be
`12.5\; {\rm \cdot m \cdot s^(-1)}` while the final vertical velocity of the ball would be
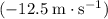`(-12.5\; {\rm m\cdot s^(-1))` right before landing (the negative sign suggests that the final velocity of the ball would be pointing downwards.)

The change in the vertical velocity of this ball would be:

`\begin{aligned} &\Delta v_(y) \\ &= (\text{final $v_(y)$}) - (\text{initial $v_(y)$}) \\ &= (-12.5\; {\rm m \cdot s^(-1)}) - (12.5\; {\rm m\cdot s^(-1)}) \\ &= (-25\; {\rm m\cdot s^(-1)}) \end{aligned}`.

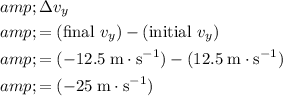The gravitational acceleration on the earth is approximately
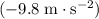`(-9.8\; \rm m\cdot s^(-2))` (negative since this acceleration points toward the ground.) The acceleration on the moon would be approximately
`a_(y) = (-1.6333\; {\rm m\cdot s^(-2)})`.

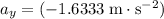Divide the change in vertical velocity by the vertical acceleration to find the duration of this projectile motion would be:

`\begin{aligned}t &= (\Delta v_(y))/(a_(y)) \\ &\approx \frac{(-25\; {\rm m\cdot s^(-2)})}{(-1.6333\; {\rm m\cdot s^(-2)})} \\ &\approx 15.31\; {\rm s} \end{aligned}`.

If air resistance is negligible, the horizontal velocity of this ball would be constant. The range of the ball (horizontal distance that the ball travelled) would be:

`\begin{aligned} & \text{range} \\ &= v_(x)\, t \\ &\approx 21.651\; {\rm m \cdot s^(-1)} * 15.31\; {\rm s} \\ &\approx 3.31 * 10^(2)\; {\rm m} \end{aligned}`.

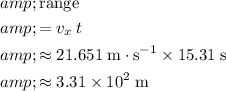Similarly, with
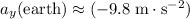`a_(y)(\text{earth}) \approx (-9.8\; {\rm m\cdot s^(-2))`, the duration of the projectile motion of this ball on the earth would be
`t(\text{earth}) \approx 2.5510\; {\rm s}` (exactly one-sixth the duration on the moon.) The range of this ball would be approximately
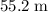`55.2\; {\rm m}` (one-sixth the range on the moon.)