Question

The water in a large lake is to be used to generate electricity by the installation of a hydraulic turbine-generator. The elevation difference between the free surfaces upstream and downstream of the dam is 165 ft. Water is to be supplied at a rate of 7000 lbm/s. The electrical power generated is measured to be 1546 hp and the generator efficiency of 92%. (1 hp = 550 lbf.ft/s).

Determine:
a. the overall efficiency of the turbine-generator.
b. the mechanical efficiency of the turbine.

Answer 1

a) 75%

b) 82%

Step-by-step explanation:

Assumptions:

`\text{The mechanical energy for water at turbine exit is negligible.} \\ \\ \text{The elevation of the lake remains constant.}`

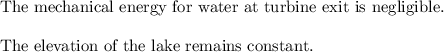
Properties: The density of water
`\delta = 1000 kg/m^3`

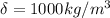
Conversions:

`165 \ ft \ to \ meters = 50 m \\ \\7000 \ lbm/s \ to \ kilogram/sec = 3175 kg/s \\ \\1564 \ hp \ to \ kilowatt = 1166 kw \\ \\`

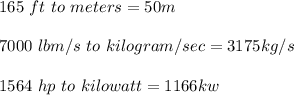
Analysis:

Note that the bottom of the lake is the reference level. The potential energy of water at the surface becomes gh. Consider that kinetic energy of water at the lake surface & the turbine exit is negligible and the pressure at both locations is the atmospheric pressure and change in the mechanical energy of water between lake surface & turbine exit are:

`e_{mech_(in)} - e_{mech_(out)} = gh - 0`

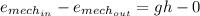
Then;

`gh = (9.8 m/s^2) (50 m) * (1 \ kJ/kg)/(1000 m^2/s^2)`

gh = 0.491 kJ/kg

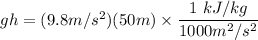
`\Delta E_(mech \ fluid) = m(e_{mech_(in)} - e_{mech_(out)} ) \\ \\ = 3175 kg/s * 0.491 kJ/kg`

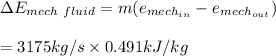
= 1559 kW

Therefore; the overall efficiency is:

`\eta _(overall) = \eta_(turbine- generator) = (W_(elect\ out))/(\Delta E_(mech \fluid))`

`= (1166 \ kW)/(1559 \ kW)`

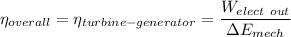
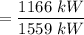
= 0.75

= 75%

b) mechanical efficiency of the turbine:

`\eta_(turbine- generator) = \eta_(turbine)* \eta_(generator)`

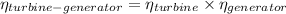
thus;

`\eta_(turbine) = (\eta_([turbine- generator]) )/(\eta_(generator)) \\ \\ \eta_(turbine) = (0.75)/(0.92) \\ \\ \eta_(turbine) = 0.82 \\ \\ \eta_(turbine) = 82\%`