Question

Show how to approximate the required work by a Riemann sum. Then express the work as an integral and evaluate it. A spherical water tank, 24 ft in in diameter, sits atop a 60 ft tower. The tank is filled by a hose attached to the bottom of the sphere. If a 1.5 horsepower pump is used to deliver water up to the tank, how long

Answer 1

The time it will take is approximately 104,128 seconds

Explanation:

The given parameters are;

The diameter of the tank, D = 24 ft.

Therefore, the tank radius, R = D/2 = 24 ft./2 = 12 ft.

The height of the tower on which the tank sits, h = 60 ft.

The hose through which the tank is filled is attached at the bottom of the tank

The radius of a slice of sphere, r = √(R² - y²) = √(12² - y²)

The power of the pump which is used to deliver the water = 1.5 horsepower

The volume of a slice of water in the tank, V = π·r²·Δx = π·(√(12² - y²))²·Δx ft³ = (144 - y²)·π·Δx ft³

The force of the slice, F = V·g·ρ = (144 - x²)·π·Δx ft³ × 62.5 lb/ft³

Let '
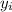`y_i`' represent the height to which each slice is pumped in the tank, we have;

y = R - (√(R² - x²)) = 12 - (√(144 - x²)

`\lim\limits_(n \to \infty)\ \sum\limits_(i=0)^n (144 - x^2) \cdot \pi * 62.5 \cdot y_i\ \Delta x \ lb`

The work done is therefore;

`W = 62.5*\pi * \int\limits^(12)_(-12) {(144 - x^2) \cdot(12-(√(144-x^2) ) \ } \, dx = 632044.366475 \ ft. \cdot lb`

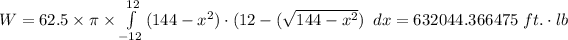
The work done in filling the tank, W = 632,044.366475 ft·lb

The work done in lifting the water to the base of the tank, W₂ = V·ρ·g×h

`\therefore W_2 = 60 * 62.5*\pi * \int\limits^(12)_(-12) {(144 - x^2) \ } \, dx = 632044.366475 \ ft. \cdot lb = 85273382.0257`

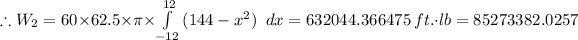
Therefore, W₂ = 85,273,382.0257 ft.lb

The total work done by the pump,

W = 85,273,382.0257 ft.lb + 632,044.366475 ft·lb = 85,905,426.3922 ft.lb

The time it will take the pump to fill the tank, 't', is given as follows;

1

Power, P = Work, W/(Time, t)

∴ t = W/P

P = 1.5 HP = 550 × 1.5 ft·lb/s = 825 ft·lb/s

t = 85,905,426.3922 ft.lb/(825 ft·lb/s) = 104,127.789566 s

The time it will take, t ≈ 104,128 seconds