Question

4. J(11,-2), K(3,-2), L(1, -7), M(1,-2)

Determine if jk and lm are parallel perpendicular or neither .

Answer 1

Based on where they both his the graph they would run PERPENDICULAR to each other

Answer 2

perpendicular

Explanation:

Calculate the slopes m of the lines using the slope formula

m =
`(y_(2)-y_(1) )/(x_(2)-x_(1) )`

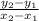
with (x₁, y₁ ) = J (11, - 2 ) and (x₂, y₂ ) = K (3, - 2 )

`m_(JK)` =
`(-2-(-2))/(3-11)` =
`(-2+2)/(-8)` =
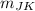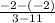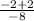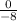`(0)/(-8)` = 0

A line with a slope of 0 is a horizontal line parallel to the x- axis

Repeat with (x₁, y₁ ) = L (1, - 7 ) and (x₂, y₂ ) = M (1, - 2 )

`m_(LM)` =
`(-2-(-7))/(1-1)` =
`(-2+7)/(0)` =
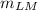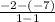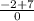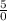`(5)/(0)` ← undefined slope

A line with an undefined slope is a vertical line parallel to the y- axis

Since JK is horizontal and LM is vertical then they are perpendicular.